The first time I saw a cubic-bezier function in my CSS I dubbed them “number barf”. I saw them as four numbers that seemed random and definitely were not a natural way to describe easing. My thoughts on them have changed greatly over the years, of course, but back then we weren’t off to the greatest start.
Realizing what those numbers represented, and how they could also be visualized as a motion graph completely changed my mind about those cubic-beziers.
Going from the function to the graph
The key to reading cubic-bezier function is that those four numbers represent two x,y coordinates: cubic-bezier(x1,y1,x2,y2);Those two coordinates can be plotted on a graph as the location of the two moveable control points that form the curve like this:
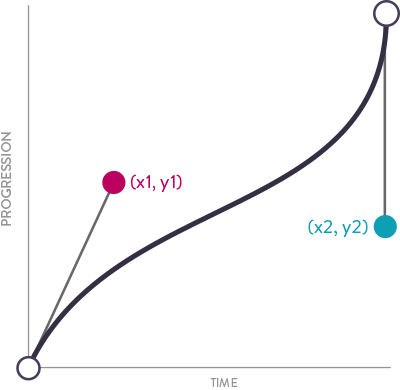
Just like in Illustrator, or other vector editing tools, the position of those handles affects the shape of the curve in between our two fixed starting and end points. The graph plots the progression of an animation over time, so we know that the animation starts at 0% and ends at 100% of its progression. The fact that those two control points can be moved around to influence the curve is how we can get so many variations for our easing from just four numbers. These graphs are normalized to a range between 0 and 1 so that they can easily be applied (behind the scenes) to any property that the curve will be used to on.
Reading the graph
This graph form of cubic-beziers is much easier to read at a glance. Where the curve is steeper, the rate of change is faster; and where the curve is flatter, the rate of change is slower. Just by looking at the shape, you get a good idea of the kind of easing it will create. (The curve pictured above will start out at a fast rate of change, slow in the middle, then speed up even more as it ends.)
It’s even easier to connect the results when you see them side-by side on cubic-bezier.com, in your browser dev tools or possibly even in your code editor if it has a cubic-bezier editor built in. Cubic-bezier.com is one of the best sites for exploring cubic-bezier function possibilities. You can adjust the curves and see both how they look in graph form and how they play out in an animation. It lets you “race” different easing curves against each other for fun too.(Spoiler alert: it’s always a tie.)
If you want to get even more in-depth with cubic-bezier functions, this Kirupa article is the thing to read. This online book gets deep into the math behind the curves, and if, like me, you prefer a visual explanation of how the curves are drawn this cubic-beziers under the hood video is extremely helpful.
This article originally appeared in the UI Animation Newsletter. Subscribe to get web animation tips and resources straight to your inbox each week!
